この記事では準1級で学習する確率過程についてわかりやすい解説とともに、応用事例についても紹介しています。
確率過程は準1級を学ぶ際に、難しい数式ばかりが並んでいて理解に苦しんだ経験があるかもしれません。
私自身も確率過程を始めて学ぶときに苦労したので、基礎的な内容を重点的に紹介しています。
確率過程とは?
確率過程とは、時間tの経過とともに変遷する確率変数\(X_t\)の経緯を統計的に分析していく手法です。
確率過程を初めて学ぶ際の基礎的なポイントは次の4つにまとめてあります
確率過程の表記方法
時間tにおける確率変数を表記する場合は次のようになります。
$$ X = (X_t)_{t\geq0} $$
\(t\)においては、離散値・連続値の両者を取り扱います。離散値の場合は、イベントが生じた回数、連続値は時間を表す事が多いです。
この表記で確率過程を表すため、まずはこれを頭に入れておきましょう。
独立定常増分過程
独立定常増分とは、次の定義になります。
(1) 任意の\(0=t_0 < t_1 < … < t_{n-1} < t_n\) に対して、\(X_{t0},X_{t1}-X_{t0},X_{t2}-X_{t1},…\)は互いに独立である。
(2) 任意の\(0<=t<t+h\)に対して、\(X_{t+h} – X_t\)の分布は\(X_h-X_0\)の分布と同一である。
難しいですが、(1)(2)の定義を極端に解釈すると次の通りになります
(1)増減値(\(X_{t1}-X_{t0}\))はそれぞれ独立である
(2)増減値(\(X_{t1}-X_{t0}\))は同一の確率分布に従う
準1級で学習する確率過程は全てこの独立定常増分という条件に基づいています。
定義自体はかなり小難しいですが、内容自体は「独立性」「同一分布」と似通っているところもありますので、それが少し形式が変わったという認識で理解するとわかりやすいです。
必要知識
確率過程を初めて学習する際は、事前に次の分布を学ぶことをおすすめします。
- ポアソン分布
- 指数分布
- ガンマ分布
これらの分布は全て、ポアソン過程の項にて、モデル式の導出において用います。
ウィナー過程(ブラウン運動)
ウィナー過程とは、\(W_t=0\)において確率過程\(W = (W_t)_{t>=0}\)が次の特性を満たしている過程のことを指します。
(1)\(W\)は独立定常増分過程である
(2)各\(t>=0\)に対して、\(W_t \sim N(0,1)\)
(3)\(W\)のパスは連続である。
特に(2)の\(W_t \sim N(0,1)\)の定義を満たしたのを標準ブラウン運動といいます。具体的に言うと \(W_{t+1} – W_t \sim N(0,1)\)、\(W_t \sim N(0,t)\)の分布に従います。
また、次のように式変形すると、\(N(μ,σ^2)\)をベースにしたブラウン運動になります。
$$Bt = μt + σW_t\sim N(μt,σ^2t) B_t- B_{t-1} \sim N(μ,σ^2) \tag{1} $$
※\( B_0 = 0 \)
ここでのポイントは、確率過程\(B_t\)は正規分布の各パラメータ\(t\)をかけた分布になっていると言うことです。\(B_t\)を表すときは次のように言い換えることもできます。
$$ B_t = (B_t – B_{t-1}) + (B_{t-1} + B_{t-2}) + … + (B_1 – B_0) = B_t – B_0 $$
独立定常分布の前提から、式(1)は\(N(μ,σ^2)\)を\(t\)回足し合わせた物と同義であるため、正規分布の再生性から\(N(μt,σ^2t)\)というように導出できます。
パラメータ推定
ブラウン運動における正規分布\((μt,σ^2t)\)の平均、分散のパラメータ推定は次の式で算出できます。これは、最尤推定法またはモーメント法で導出できます。
$$ μΔ = \frac{1}{n}\displaystyle \sum_{i=1}^{n}Z_i \tag{4} $$
$$ σ^2Δ = \frac{1}{n}\displaystyle \sum_{i=1}^{n}z_k^2 – (μΔ)^2 \tag{5} $$
$$Z_k := B_{kΔ} – B_{(k-1)Δ} \sim N(μΔ , σ^2Δ) $$
\(Δ\)は時間間隔、\(Z_k\)は時間間隔\(Δ\)におけるデータ\(B_k\)の差を表しています。
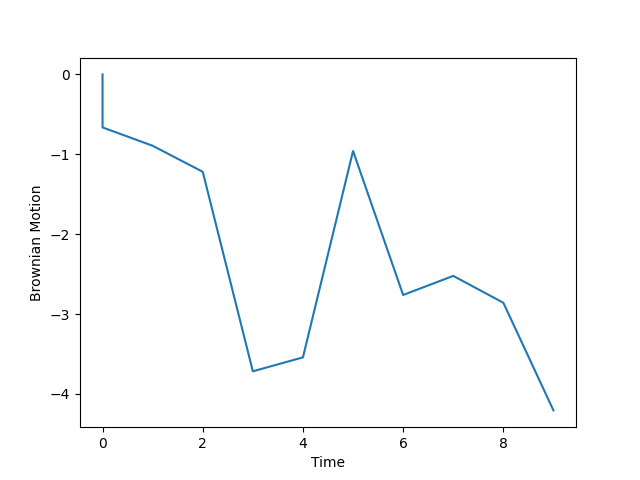
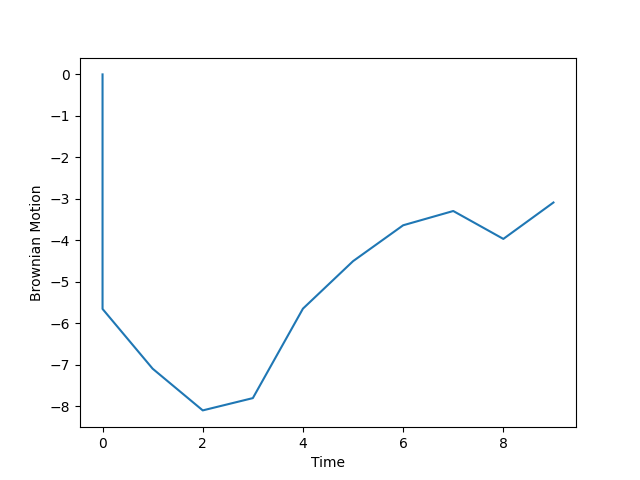
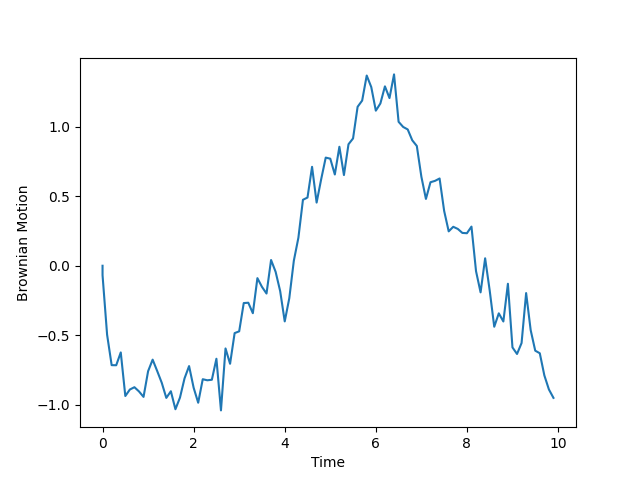
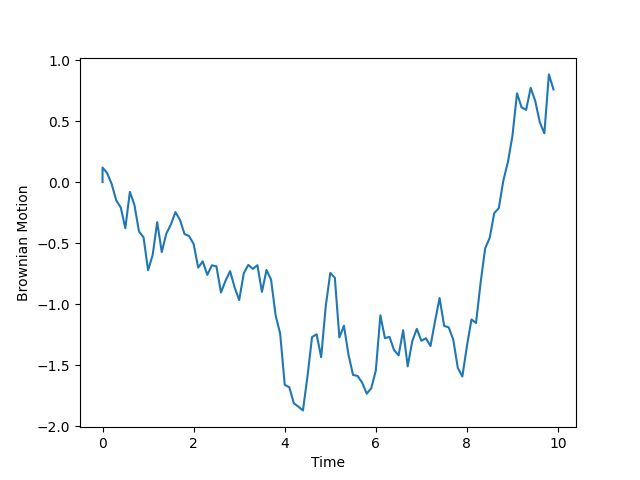
平均、分散の式の両辺を時間間隔\(Δ\)で除算することにより、パラメータを推定することができます。\(Δ\)は基本的に1をとる場合が多いですが、高頻度観測によって時間間隔\(Δ\)が0.01と問題に設定される場合があります。\(Δ\)が0.01~1では次の図のようにばらつきに差があることが分かります。
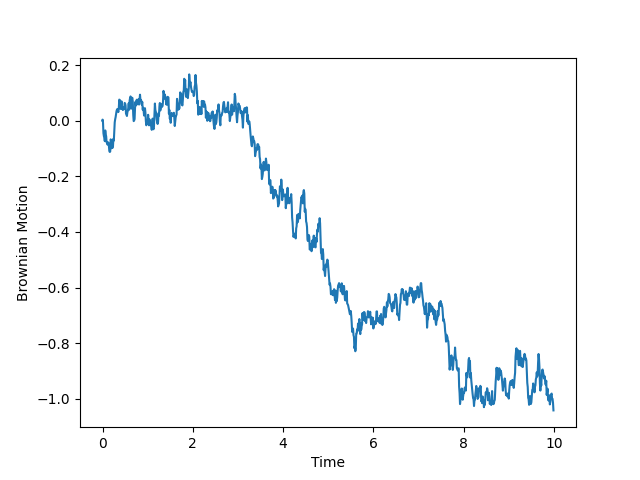
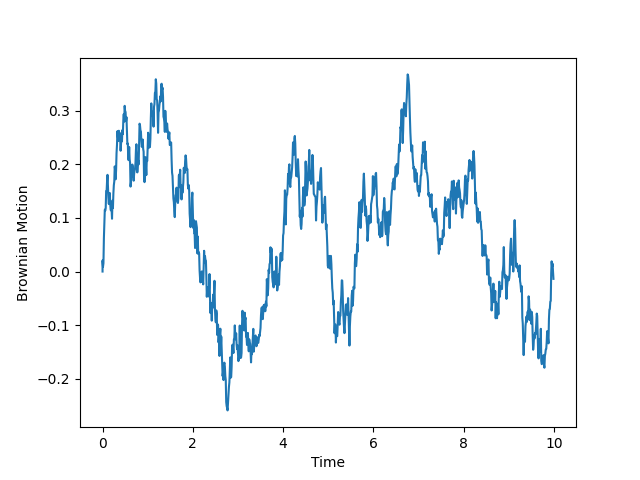
ポアソン過程
ポアソン過程とは、各\(t\)で自然数をとる確率過程\(N = (N_t)_{t>=0}\)が次の特性を満たしている過程のことを指します。
(1)\(N\)は独立定常増分過程である
(2)任意の\(t\geq0\)に対して、\(N_t\)は強度\(λt\)のポアソン分布に従う。
確率過程の式は次のように定義されます。
$$P(N_t = k) = e^{-λt}\frac{(λt)^k}{k!} , k= 0,1,2,… \tag{6}$$
この過程は、まれに生じるイベント\(N_t\)が時間\(t\)と連動するモデルで主に地震や自動車事故の発生回数のモデルに用いられています。さらに、ポアソン過程は、後に述べる複合ポアソン過程に応用されています。
パラメータ推定
ポアソン過程のパラメータ\(λ\)の推定には2通りの方法が存在します。
(1) イベントが生じた時刻\(T_1,T_2,…,T_n\)の観測をする
(2) 時間間隔Δによって、データ\(N_0,N_Δ,N_{2Δ},…,N_{nΔ}\)の観測をする
(1)の算出式は次の通りになります。
$$λ = \frac{n}{Tn} $$
(2)の算出式は次の通りになります。
$$λ = \frac{NnΔ}{nΔ} $$
(1)(2)のポイントは、いずれのデータであっても次の式でパラメータが算出できると言うことです。
$$ λ = \displaystyle \frac{(イベントの総回数)}{(観測時間)}$$
従来通りの計算方法で計算できるため、覚えやすいと思います。
複合ポアソン過程
複合ポアソン過程とは、ポアソン過程を用いた応用例で次の式で表します。
$$ X_t = \displaystyle \sum_{k=1}^{N_t}U_k \tag{7} $$
\(N = (N_t)_{t\geq0}\)のポアソン過程で\((U_k) k=1,2,..\)は互いに独立の同一分布に従う確率変数で、\(N\)とも独立とします。
このモデルの意味は、「\(k\)回目のイベントにおいて何かしら生じた\(U_k\)の総和」と解釈でき、発生回数とあるイベントについて考察することができるようになります。
パラメータ推定
パラメータ推定は条件付き期待値をとって計算します。計算過程は複雑ですが、\(N_t\)と\(U_k\)は独立事象という観点から計算していくと意外とシンプルに計算できます。
\( E[N_t] = λt 、E[U_k] = μ 、V[U_k] = σ^2\)とすると、
\(E[X_t] = E[E[\displaystyle \sum_{k=1}^{N_t}U_k|N_t]] = E[\displaystyle \sum_{k=1}^{N_t}E[U_k|N_t]] \)
\(= E[\displaystyle \sum_{k=1}^{N_t}E[U_k]]\)
\(= E[N_tμ] = λμt\)
\(E[X_t^2] = E[E[(\displaystyle \sum_{k=1}^{N_t} U_k)^2|N_t]]\)
\(= E[E[\displaystyle \sum_{k=1}^{N_t}U_k^2 + 2\displaystyle \sum_{j>i}^{}U_iU_j|N_t]] \)
\(= E[E[(σ^2 + μ^2)N_t + μ^2N_t(N_t-1)]] \)
\(= σ^2E[N_t] + μ^2E[N_t^2] = σ^2λt + μ^2[λt+(λt)^2] \)
よって、
\(V[X_t] = E[X_t^2] – (E[X_t])^2 = λt(μ^2 + σ^2) \)
このようにして、ポアソン過程モデル\(N_t\)で生じるイベント\(U_k\)の総和を複合ポアソン過程にて求めることができます。
確率過程の利用例
ランダムウォーク
金融分野ではランダム・ウォークの理論が利用されています。これは、株価や金融商品の上がり下がりは全て規則的に動いているのではなく、「ランダムに」変動しているという仮説です。
この理論を通して、世間で広まっている法則が株価の予測につながらないという結論を導いています。
待ち行列理論
待ち行列理論とは、スーパーのレジや銀行のATMで発生する行列を解析する理論のことを指します。待ち行列理論の一つにポアソン過程のモデルが用いられます。
待ち行列理論を用いて解析することにより、人材や機械のコストを抑えつつ、最適な方法について考察できるようになります。日常の中でも統計学が用いられているのはとても面白いですね。
保険数理
例えば、事故が生じる回数を\(N_t\)というポアソン過程の仮定を置き、事故で生じる請求額が\(X_k\)というある確率分布に従う場合、請求額の総和\(\sum_{k=1}{N_t}X_k\)はどれだけの物になるのかを複合ポアソン仮定で予測することができます。
結論
確率過程について解説しました。
確率過程は「独立定常増分」を前提にしてモデルが構築されており、金融分野や工学分野、保険数理学といった幅広い分野で活用されています。
確率過程の学びとともに、その面白さについて体感してもらえれば幸いです!


コメント