この記事では、統計学の基本となる仮説検定についての最適なサンプリングサイズ設計について第一種の過誤と検出力の二つの面から解説していきます。
検定では「第一種の過誤(type I error);\(α\)」と「第二種の過誤(type II error);\(β\)」の二つが相反関係で同時に小さくすることが難しい問題があります。
その問題を解決するためにはサンプルサイズを大きくすることが必要です。第一種の過誤を抑えたまま検出力(1-β)を大きくすることができます。
しかし、サンプルサイズをどれくらい大きくすればいいか分かりません。そこで、サンプルサイズを検出力を考慮して設計する方法を紹介します。
検定における基本要素
Point
サンプルサイズ設計を学ぶためには仮説検定における過誤(error)を正しく理解し、それらの位置関係を理解することが必要です。
「第一種の過誤」と「第二種の過誤」
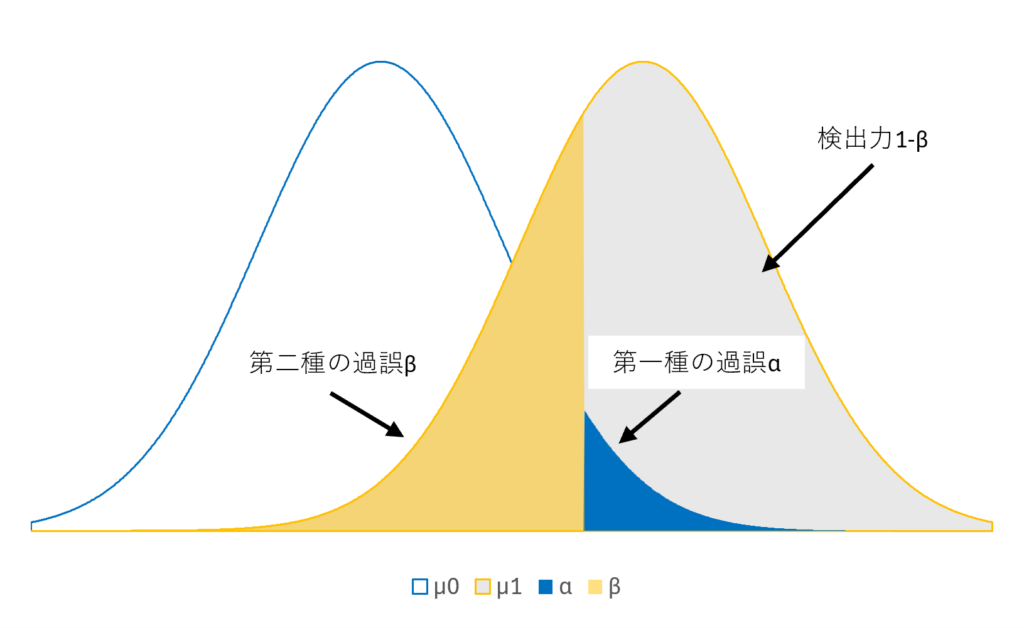
仮説検定の基礎について振り返ってみます。第一種の過誤、第二種の過誤のそれぞれは次のことを指します。
第一種の過誤:帰無仮説\(H0\)が正しい場合、帰無仮説\(H0\)を棄却する確率\(α\) :青色の領域
第二種の過誤:対立仮説\(H1\)が正しい場合、帰無仮説\(H0\)を受容する確率\(β\) :橙色の領域
また、対立仮説\(H1\)が正しい場合、帰無仮説\(H0\)を棄却する確率を検出力\(1-β\)といいます。
優れた仮説検定とは有意水準\(α\)を低く保ったまま、検出力\(1-β\)を一定の高い設定にすることを指します。
第一種の過誤は「任意に決められる」
第一種の過誤は私たちが有意水準というかたちでコントロールできます。有意水準は両側・片側そして、10%、5%、1%というように自らが対象によって設定することができます。
有意水準を低く設定することで、第一種の過誤が生じる確率を下げることができます。しかし、有意水準を低く設定すると別の問題が生じてしまいます。
第二種の過誤は「第一種の過誤とトレードオフ」
第二種の過誤は第一種の過誤とトレードオフの関係にあります。つまり、有意水準を低く設定すると相反して第二種の過誤が増加します。
よって、第一種の過誤と第二種の過誤を同時に低く設定することは難しい問題があります。もし、第二種の過誤が高い確率の場合にテストを実施すると、帰無仮説を棄却してもその対立仮説を受容する信頼性が低くなります。
この問題を対応するためには、仮説検定に用いるサンプルサイズを増加させることが必要です。しかし、サンプルサイズを増やすといってどれくらい増やせばいいのか分かりません。
サンプルサイズ設計について
Point
サンプルサイズを増やすことでそれぞれの過誤を抑えられる反面、サンプルを収集するコストが増加します。
これらの問題に対応するためには、私たちが望む有意水準や検出力下におけるサンプルサイズを選択する必要があります。
検出力を利用したサンプルサイズ設計
検出力を考慮したサンプルサイズの設計は次の式で求めることができます。
$$ n = \frac{(z_{a/2} – z_b)^2}{\frac{(μ_1-μ_2)^2}{σ^2}} = \frac{(z_{a/2} – z_b)^2}{Δ^2} \tag{1} $$
\(n\)はサンプルサイズ、\(z_{a/2}\)、\(z_b\)はそれぞれ標準正規分布における上側\(100\frac{α}{2}\)%点、\(100β\)%点。\(μ_1\)、\(μ_2\)はそれぞれ帰無仮説\(H0\)、対立仮説\(H1\)における平均、\(Δ^2\)はエフェクトサイズになります。
\(Δ\)は数式から、\(\frac{(μ_1 – μ_2)}{σ}\)によって計算し、これは平均値の差が標準偏差の何倍に相当するか表しています。式から、エフェクトサイズが小さい(=平均の差が小さい、または標準偏差が大きい)と検出力が低くなってしまいます。
式の導出
次式を導出するためには帰無仮説と対立仮説における分布の位置関係を正しく理解することが必要です。
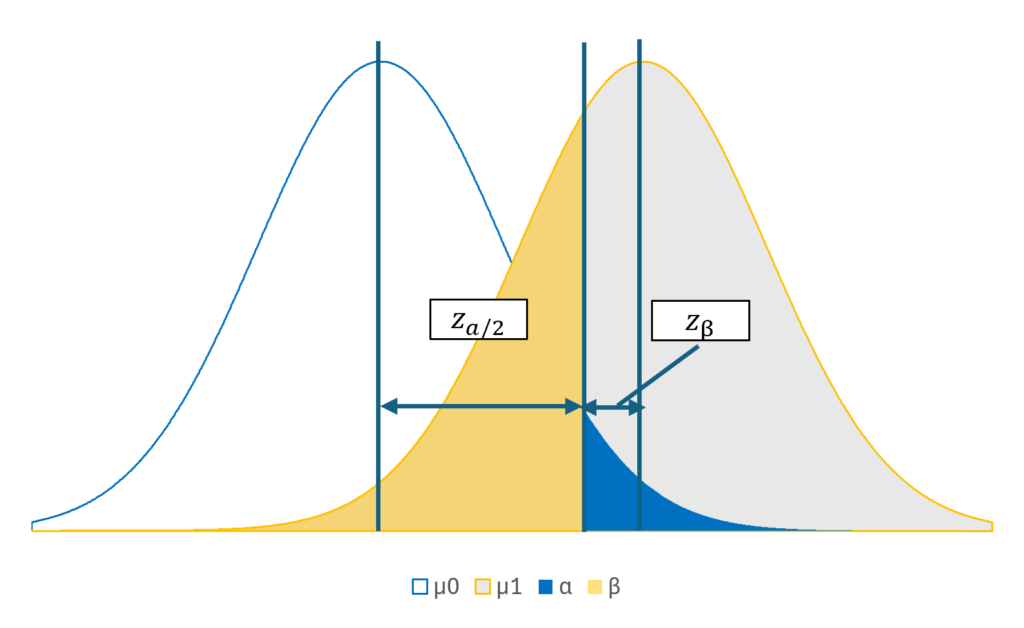
帰無仮説\(H0\)で設定する有意水準\(α\)の分位点と平均値\(μ_0\)との距離が\(z_0\)に相当します。次に、対立仮説\(H1\)の検出力\(1-β\)を確保することを考えた場合、有意水準\(α\)の分位点の左側(橙色の領域)が確率\(β\)に相当するような設定にしなければなりません。
つまり、有意水準\(α\)の分位点と対立仮説\(H1\)の平均との距離は確率\(β\)を保有する\(z_1\)に相当する距離となります。
ここから、\(z_0\)と\(z_1\)の加算は、\(\frac{μ_1 – μ_2}{\sqrt{σ^2/n}}\)に相当することが分かります。つまり、
$$ z_{α/2} + z_β = \frac{μ_1 – μ_2}{\sqrt{\frac{σ^2}{n}}} \tag{2} $$
となります。そして、\(n\)について解くことによって式(1)が得られます。
具体例1:検出力の計算
検出力の計算は、\(z_β\)について解き、正規分布表から確率を計算することで求められます。まず、\(z_β\)の分位点を計算する式は次の通りになります。これは、式(2)の\(z_α\)を右辺に移項した式で計算できます。
$$ z_β = \frac{μ_1 – μ_2}{\sqrt{\frac{σ^2}{n}}} – z_{α/2} \tag{3} $$
計算していくと、\(z_β = 0.67\)となります。ここから、標準正規分布表の確率を求めると、\(β = 0.2514\)。つまり、検出力は\(1-β = 0.7486\)となり、約75%になります。まずまずの結果なっています。
具体例2:サンプルサイズの計算
先ほどの例を展開し、検出力を80%以上にするサンプルサイズの計算を考えてみます。
帰無仮説\(H0\):\(μ_0 = 100\)
対立仮説\(H1\):\(μ_1 = 102\)
と先ほどと同じ仮定を置きます。今回は、サンプルサイズを計算するため、式(1)を使います。検出力80%の分位点\(z_β\)は標準正規分布表から0.84と算出できます。
その値を用いて、計算すると\(n = 111\)となります。
結論
仮説検定の信頼性を高めるためにはサンプルサイズを増やし、有意水準を低い維持したまま検出力を確保する必要があります。
検出力の計算を理解するためには、帰無仮説と対立仮説の位置関係を正しく理解することが必要です。すると、この計算式の導出について理解しやすくなります。
サンプルサイズ計算自体は簡易的ですが、なぜそのように求めるか考えると少し混乱してしまいます。この記事を参考に理解の手助けになれば幸いです!



コメント